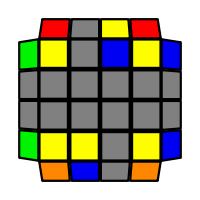
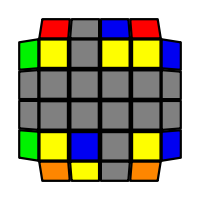
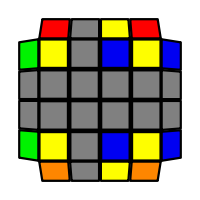
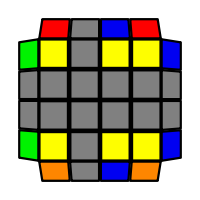
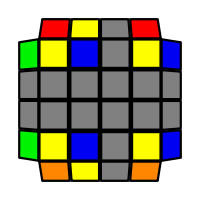
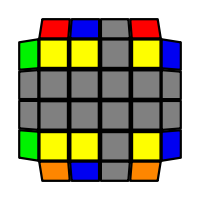
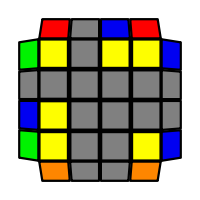
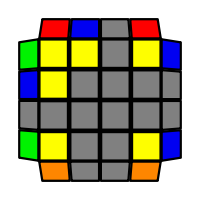
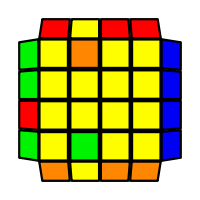
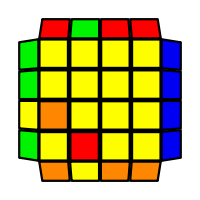
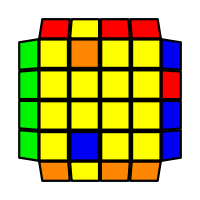
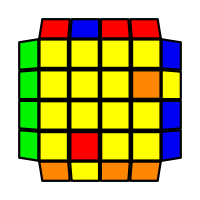
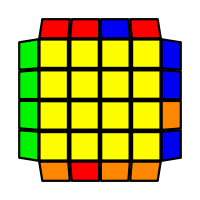
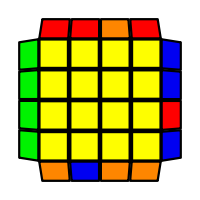
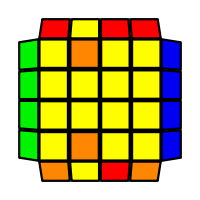
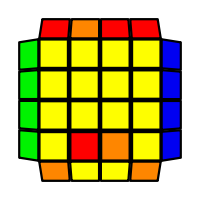
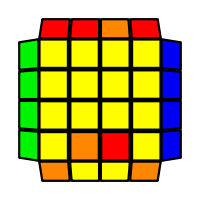
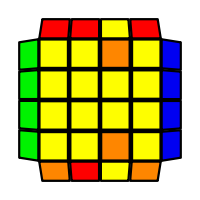
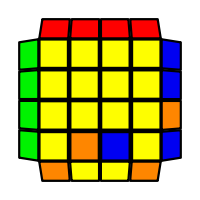
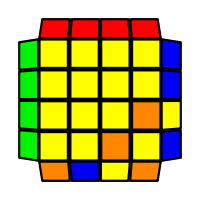
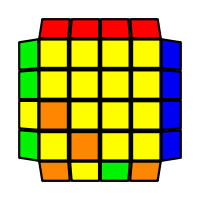
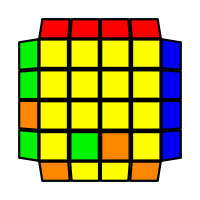
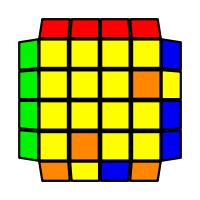
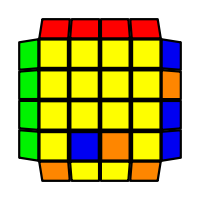
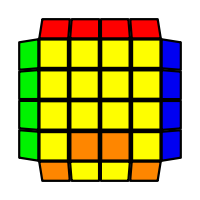
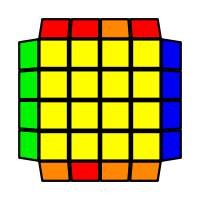
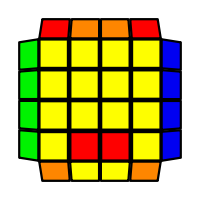
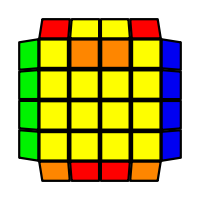
I will outline the general approach I use in this step along with some algorithms that I use. You can learn these algorithms like any other, but it would be a waste of your time - they're all pretty similar and you should be able to derive your own to do different things from the first few you learn. The algorithms are listed to provide you with hopefully nicer alternatives if you find bad ones, to show you various tricks you can employ to manipulate edges and to show you how to do cases you may not have worked out youself. Study them, but don't learn them. If you read this page and get completely lost, this entire step can be completed with only two algorithms (the first 3-cycle and any of the 2-cycles), however - this won't be very quick at all. As with F3L, algorithms that work on the 3x3x3 apply here aswell. It might be worth learning full 3x3x3 ELL, since it sure comes in handy when you have accidentally paired edges. I use a general method that allows me to complete this step in no more than 3 algorithms each time. I sometimes deviate from this system and go freestyle if I see an obviously nicer solution. I used to use a purely freestyle system, solving 2 or more edges each time - but this led to too much thinking and not enough time solving. With a set system, you know each step and what to do each time without having to think about it, and you can automatically execute. The general idea is; solve an edge pair with the first algorithm (this means pairing it and inserting it to the correct slot), solve another edge pair with the second algorithm (opposite or adjacent), and solve the last two edge groups in a single algorithm. There are only 24 different configurations for the last two edges and it's really worth learning how to solve each of them. Most of the 24 configurations are algorithms you will likely already know, you'll just need to learn things like the 4-cycles. I've listed a set of algorithms that will help you understand how solving the first and second edges should be accomplished, after that I have listed general purpose algorithms for you to deploy at any stage in this step. Some are simply listed for completeness, as you can sometimes solve a 2x2-cycle faster by using 2 3-cycles. Not every case will be documented, but you should be able to solve cases that are not with the tricks shown in documented cases. There's a document created by Christopher Mowla here that lists all the 3-cycles and how they're related. Of course, I haven't listed every case. Discovery is half the fun! If you find a case you can't seem to solve, drop me an email or hop on IRC and I'll help you out. Some of the following algorithms are written in commutator or conjugate notation. With this notation, [X,Y] translates to XYX'Y', and [X:Y] translates to XYX'.
|